問題番号009　　解答編

2009年3月19日に寄せられた yas さんの解答がとてもスマートでした。

解答一例（かなり遠回り）



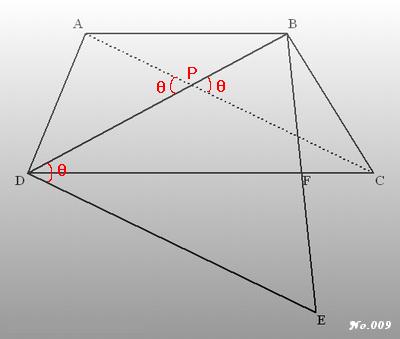
台形ABCDの2つの対角線の交点をＰとし、∠BPC＝θ、
台形ＡＢＣＤの面積をS₁とする。
S₁＝（△BPCの面積）+（△APBの面積）+（△APDの面積）+（△CPDの面積）。
ここで、∠APDは∠BPCの対頂角なので、∠APD＝θ。

∴（△BPCの面積）＝（1/2）・BP・CP・sinθ
（△APBの面積）＝（1/2）・AP・BP・sin（180°－θ）＝（1/2）・AP・BP・sinθ
（△APDの面積）＝（1/2）・AP・DP・sinθ
（△CPDの面積）＝（1/2）・CP・DP・sin（180°－θ）＝（1/2）・CP・DP・sinθ

したがって、S₁＝（1/2）（BP・CP+AP・BP+AP・DP+CP・DP）sinθ
＝（1/2）{BP（AP+CP）+DP（ＡＰ+CP）}sinθ
＝（1/2）（BP+DP）（AP+CP）sinθ
＝（1/2）・BD・AC・sinθ。



△BDEの面積をS₂とすると、
S₂＝（1/2）・DB・DE・sin∠BDE。

ここでAC//DE、∠BDEと∠BPCは同位角なので
∠BDE＝∠BPC、すなわち∠BDE＝θ。

また、DE＝ACなので、
S₂＝（1/2）・DB・DE・sin∠BDE
＝（1/2）・BD・AC・sinθ。

∴　S₁＝S₂　・・・①

台形ABCDと△BDEの共通部分△BDEの面積を①の両辺から引くと、
S₁－（△BDEの面積）＝S₂－（△BDEの面積）
⇔（△ABDの面積）+（△BCFの面積）＝（△DEFの面積）



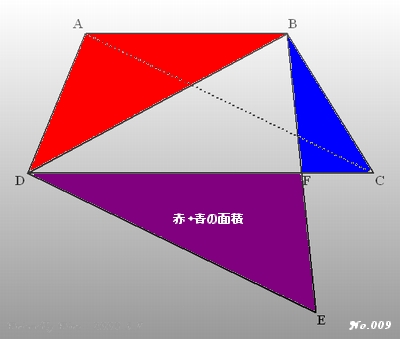
ここで、（△ABDの面積）＝200、（△BCFの面積）＝40なので
（△DEFの面積）＝200+40＝240。

したがって、△BCFの面積は△DEFの面積の（40/240）倍、
すなわち（1/6）倍である。


答え：1/6倍



ちょっと一言：
図形の面積比で解こうとした人がいっぱいいると思います。
しかし、その手法では数のわからない文字が逆に増える一方で答えに辿り着かないでしょう。
（CEに補助線を引いて解こうとしているのは、ひっかかっている証拠でしょう。）
問題文の「△BCFの面積は△DEFの面積の何倍か求めよ。」というのは、そうさせるための罠です。

残念ながら今回は正解者0名でした。


追記（2009年3月20日）：
私の見落としで、上のような生意気な一言を述べたことをお詫びします。
yas さんのご指摘で、面積比でも解けることに気がつきました。
yas さん、本当にありがとうございました。
これからも綺麗で面白い問題作りに励んでいきたいと思います。


戻る