問題番号006 解答編

(i) 1回で終了するとき
1通りしかないので確率は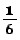 となる。
となる。
(ⅱ)2回で終了するとき
1回で終了しない確率は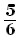 で、そこか
らゴールする確率が
で、そこか
らゴールする確率が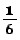 な
ので、
な
ので、
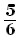 ×
×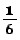 =
= 確率
は
確率
は と
なる。
と
なる。
(ⅲ)3回で終了するとき
1回で終了しない確率は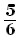 、2回目で
終了しない確率が
、2回目で
終了しない確率が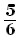 で、
そこからゴールする確率が
で、
そこからゴールする確率が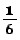 なので
なので
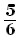 ×
×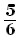 ×
×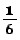 =
= 確率は
確率は となる。
となる。
同様にしてn回で終了するときを考えると、
n-1回目まで終了することはなく、n回目に終了するので
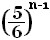 ×
×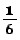 =
=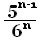 した
がってn回で終了する確率は
した
がってn回で終了する確率は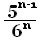 となる。
となる。
1回からn回までの回数の期待値を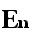 とすると、
とすると、
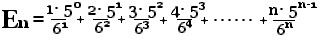 で
ある。
で
ある。 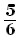 =r とお
くと・・・
=r とお
くと・・・
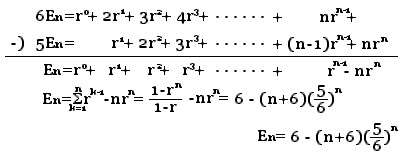
nは無限まで存在するので、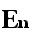 の極限を調
べる。
の極限を調
べる。
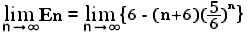
ここで、
(n+6)(5/6)^n≦7・(8/7)^(n-1)・(5/6)^n=(49/8)・{(8/7)・(5/6)}^n=(49/8)(20/21)^n
すなわち (n+6)(5/6)^n≦(49/8)(20/21)^n (nは自然数)・・・・・・① と推測できる。
----証明----
[1] n=1のとき ①において、(左辺)=(35/6) (右辺)=(35/6)
よって、n=1のとき①は成り立つ。
[2] n=k(kは自然数)のとき ①が成り立つと仮定すると、
(k+6)(5/6)^k≦(49/8)(20/21)^k ・・・・・・②
n=k+1のとき ①において、
(左辺)={(k+1)+6}・(5/6)^(k+1)={5(k+7)/6}・(5/6)^k={5(k+7)/6(k+6)}・(k+6)・(5/6)^k
≦{5(k+7)/6(k+6)}・(49/8)・(20/21)^k={5(k+7)/6(k+6)}・(21/20)・(49/8)・(20/21)^(k+1)
={7(k+7)/8(k+6)}・(49/8)・(20/21)^(k+1)≦(49/8)(20/21)^(k+1)=(右辺)
∵ {7(k+7)/8(k+6)}において、
kは自然数であるから k≧1 ⇔ 7(k+7)≧8(k+6) ⇔ {7(k+7)/8(k+6)}≦1 であることより。
よって、n=k+1のときにも①は成り立つ。
[1] [2] より、すべての自然数nに対して①が成り立つ。 ①(証明終了)
また明らかに、(5/6)^n<(n+6)(5/6)^n である。 ∵ n+6>1より
∴ (5/6)^n<(n+6)(5/6)^n≦(49/8)(20/21)^n ・・・・・・③
③式において、第1辺の極限は0、第2辺の極限も0である。
したがって、ハサミウチの原理より 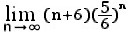 =0。
=0。
よって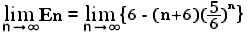 =
6-0=6 極限値は6をとるので、
=
6-0=6 極限値は6をとるので、
求める期待値は
6回
である。
追記(2009年3月10日):
解答をご覧になった方、本当に申し訳ございません。
2008年3月12日に発表した解答に不備があったので、赤字の部分を付け足しました。
発表当時、極限のハサミウチをまだ習っていなかったので、曖昧な解答となってしまいました。
お手数かけてすみませんが間違いなどを発見された方は、
どうぞトップページの下部メールアイコンからよろしくお願い致します。
戻る