問題番号005　解答編


解答一例（他に簡単な方法もあります＾＾；）



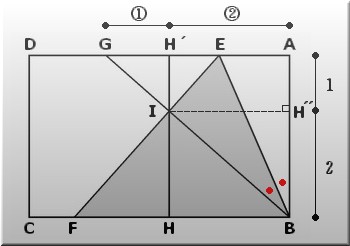
GH´：H´A＝1：2　より　AB＝ 3IH´
AB＝H´I + IH　より　3IH´＝IH´ + IH
2IH´＝IH ＝2。　よって IH´＝1　AB＝3。

IH´´⊥ABとなるAB上の点H´´をとる。
このとき、△ABE≡△IBEより　AB=IB　なので　IB＝3　H´´B＝IH＝2。

∠ABE＝∠EBI＝αとする。



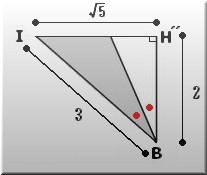
△IH´´Bにおいて
三平方の定理より　IB²＝BH´´²+IH´´²
9＝4 + IH´´²   IH´´²＝5　　IH´& acute;＞0より　 IH´´＝√5 となる。

また、余弦定理より
IH´´²＝IB²+BH´´² -2IB・BH´´cos2α
5＝9+4-12cos2α　　12cos2α＝8　　cos2α＝ ²/₃。

加法定理より
cos2α＝2cos²α -1　　　²/₃ ＝2cos²α -1　　2cos²& alpha;＝ ⁵/₃　　cos²& alpha;＝ ⁵/₆。

三角比の相互関係より
tan²α +1 ＝　１／cos²& alpha;　　tan²α +1 ＝ ⁵/₆　 　tan²& alpha;＝ ¹/₅ 。



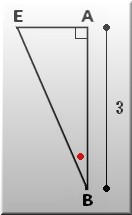
△ABEにおいて
AE／AB ＝tanα より　AE＝ABtanα
AE²＝AB²tan²& alpha;　　AE²＝9・¹/₅ ＝ ⁹/₅ 。



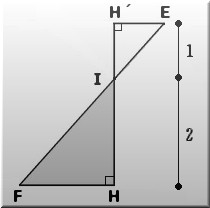
△ABE≡△IBEより  AE=EI。

△H´IEと△HIFにおいて　∠H´IE＝∠HIF　∠ IH´E＝∠IHFなので
それぞれの２角が等しいことより　△H´IE∽△HIF。
また、H´I：IH＝1：2 より　IF＝2EI。
AE²＝EI²　　IF²＝4EI²　 より　　IF²＝4・⁹/₅＝ ³⁶/₅　。



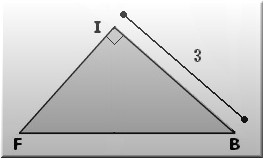
△ABE≡△IBEより　∠EAB＝∠EIB＝90°
∠FIB＝180°-∠EIB＝180°-90°＝90& deg;

△BIFにおいて
三平方の定理より
FB²＝IB²+IF²＝9+ ³⁶/₅　＝ ⁸¹/₅ 。　　FB＞0より　FB＝　⁹／_√5。



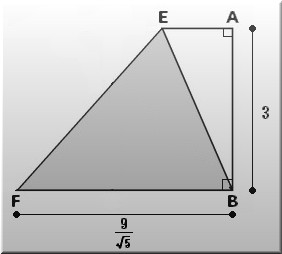
△BEFにおいて
面積は　¹/₂ ・AB・FB　であるから
¹/₂ ・3・ ⁹／_√5 ＝　²⁷／_2√5 ＝　^27√5／₁₀ 。


^答え

戻る