問題番号003　解答編


円周率が３．１０より大きいことを証明せよ。

---解答---
半径１の円に内接する正二十四角形があるとき、

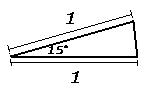
上図のような三角形が２４個あることになる。

加法定理より
sin15°=sin(60°－45°) =sin60°cos45°－ cos60°sin45°
= ｛√（６）－√（２）｝／４

したがって図の三角形の面積は、
１／２　・１・１・　｛√（６）－√（２）｝／４　＝｛√（６）－√ （２）｝／８となる。
ゆえに正二十四角形の面積は３｛√（６）－√（２）｝。

√（２） ＜1.41422    √（６）＞2.44948 　なので
√（６）－√（２）　＞1.03526
３｛√（６）－√（２）｝　＞3.10578
円に内接している正二十四角形が３．１０より大きいので
πr^2＞３．１０　　ｒ=1なので
π＞３．１０

したがって円周率は３．１０より大きい。

戻る