問題番号002　解答編




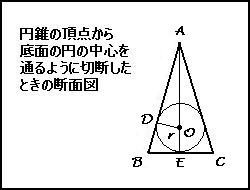
Ⅰ.ⅰ 円錐のにおいて、上図のようにA,B,Cをとり、ＡＢと球の接点をＤ、ＢＣと球の接点をＥ、球の中心をＯ、半径をｒとする。
問題文より、AB=3k  BC=2k （kは比例定数）なので、BE=kである。

ⅱ△ABEと△AODにおいて
∠AEB=∠ADO=90°（円の接線より）、　∠BAE=∠OAD （共通の角）　より、それぞれの２つの角が等しいので △ABE∽△AODとなる。

Ⅱ.ⅠよりAB：BE＝AO：OD、　よって3k：k＝｛2√(2)k－ｒ｝：ｒなので、
3kr=2√(2)k^2 －kr
3r=2√(2)k－ｒ
4r=2√(2)k
r=k/√(2)となる。

Ⅲ.円錐の表面積において

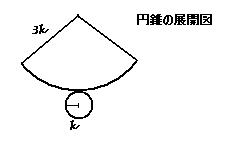
底面部分の面積はk^2 π。
扇形の弧の長さは2kπであるから、この扇形は半径3kの円の 1/3の大きさとわかる。
したがって、扇形の面積は 1/3 ・ 9k^2 π =3k^2 π。
よって円錐の表面積は 4k^2 πとなる。

Ⅵ.球の表面積において
Ⅱより、球の半径が k/√(2) なので、表面積は 4πr^2 = 4π ・ k^2 / 2 =2k^2 πとなる。


以上のことより、円錐と球の表面積の比は 4k^2 π ： 2k^2 π　＝２：１。

答え：　円錐の表面積：球の表面積＝ ２：１

戻る