問題番号001　解答編



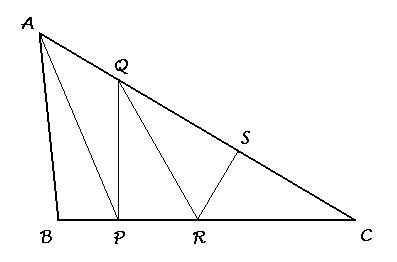
BP=3  RS=4  BC⊥QP

Ⅰ.△ABP と△APCの面積比は１：４。
この２つの三角形は高さが同じなので、底辺の長さの比が１：４となる。
したがってＰＣ＝１２。

△PQRと△QRSの面積比は１：２。
この２つの三角形も高さが同じなので、底辺の長さの比が１：２となる。
したがってPR=4  RC=8。

Ⅱ.△PQR と△SQRにおいて
ⅰ. Ⅰより、ＰＲ=SR=４　QR=QR（共通）　面積が等しい　ので
△PQRの面積は　（1/2）・PR・QR・sin∠PRQ
△SQRの面積は　（1/2）・SR・QR・sin∠SRQ
よって、（1/2）・PR・QR・sin∠PRQ＝（1/2）・SR・QR・sin∠SRQ。
ゆえに、sin∠PRQ=sin∠SRQ……①

ⅱ. このとき∠PRQ＋∠SRQ＜１８０°……②（SはRC 上にあってはならないことより）
∠PRQ＜９０°（BC⊥QPの∠QPR=９０°より）　なので、
∠SRQ＜９０°のときと　　９０°＜∠SRQ＜１８０°の場合が考 えられる。

ⅲ. しかし、９０°＜∠SRQ＜１８０°の場合、
①式より、∠SRQ＝　（１８０°－∠PRQ）となる。
これは、∠PRQ＋∠SRQ＝１８０°となってしまい、②式に矛盾するので、
９０°＜∠SRQ＜１８０°は成り立たない。
したがって∠SRQ＜９０°となり、∠PRQ=∠SRQとなる。

ⅳ. △PQRと△SQRにおいて
２辺とその間の角が等しいので、△PQR≡△SQR。

以上のことより、∠RSC=９０°

Ⅲ.△SRC において
RS=4  RC=8　より、cos∠SRC=1/2
したがって、∠SRC=６０°、sin∠SRC=√(3) /2　となる。
△SRCの面積は、（1/2）・SR・RC・sin∠SRC=8√(3)…& hellip;③


③式より、△ABCの面積を５等分したものの面積が8√(3) なので、
△ABCの面積は、5・8√(3)＝４０√(3)　となる。

答え：４０√ (3)

戻る